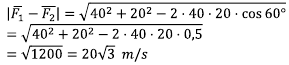Berikut ini , Soal Essay LKS Fisika tentang (Vektor) Kurikulum2013, beserta kunci Jawabannya, untuk siswa SMA/SMK/MA/Sederajat.
Soal Essay 1-10
1. Dua buah vektor masing-masing F1 = 15 satuan dan F2 = 10 satuan mengapit sudut 60°.

Tentukan arah resultan kedua vektor!
Pembahasan!
Langkah pertama tentukan dulu besar resultan vektornya:

Yang dimaksud arah resultan adalah sudut β pada gambar di bawah:

Dengan rumus sinus:

diperoleh arah resultan:

2. Dua buah vektor gaya masing – masing 8 N dan 4 N saling mengapit sudut 120°. Tentukan besar resultan kedua vektor tersebut!
Pembahasan!
Data:
F1 = 8 N
F2 = 4 N
α = 120°
R = ……..
Seperti soal pertama hanya berbeda sudut antaranya, dengan rumus yang sama:

Diperoleh hasil

Catatan rumus:
cos (180° − α) = − cos α
Sehingga untuk nilai cos 120°:
cos 120° = cos (180° − 60°) = − cos 60° = − 1/2
3. Diberikan 3 buah vektor F1=10 N, F2 =25 N dan F3=15 N seperti gambar berikut.

a. Resultan ketiga vektor

Vektor yang dalam perhitungan selanjutnya tidak digunakan lagi karena sudah diuraikan tadi, dihapus saja, agar kelihatan lebih bersih, sisanya seperti ini:
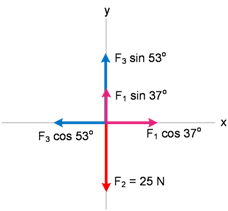
Jumlah komponen vektor-vektor pada sumbu x dan y :

b. Mencari sudut yang terbentuk antara resultan vektor R dengan sumbu x
tan θ = ΣFy /ΣFx
tan θ = −7/−1 = 7
θ = arc. tan 7 = 81,87°
4. Sebuah perahu menyeberangi sungai yang lebarnya 180 m dan kecepatan airnya 4 m/s. Bila perahu diarahkan menyilang tegak lurus dengan kecepatan 3 m/s, tentukan panjang lintasan yang ditempuh perahu hingga sampai ke seberang sungai! (Sumber Soal : UMPTN)
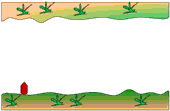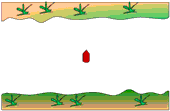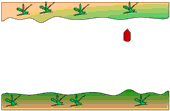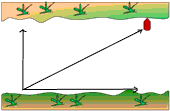


5. Perhatikan gambar gaya-gaya di bawah ini!

“Untuk dua buah vektor dengan besar yang sama dan membentuk sudut 120o maka resultan kedua vektor besarnya akan sama dengan besar salah satu vektor”
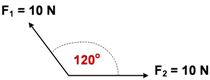
 Pada soal di atas, 2 buah vektor (gaya) masing-masing 3 N membentuk sudut 120o, sehingga resultan kedua gaya juga 3 N. Resultan kedua gaya ini akan segaris dengan gaya 6 N, namun berlawanan arah. Sehingga dengan mudah soal ini bisa dijawab resultan ketiga gaya adalah 6 N dikurangi 3 N hasilnya adalah 3 N.
Pada soal di atas, 2 buah vektor (gaya) masing-masing 3 N membentuk sudut 120o, sehingga resultan kedua gaya juga 3 N. Resultan kedua gaya ini akan segaris dengan gaya 6 N, namun berlawanan arah. Sehingga dengan mudah soal ini bisa dijawab resultan ketiga gaya adalah 6 N dikurangi 3 N hasilnya adalah 3 N.6. Diberikan 3 buah vektor :
b = 4i + 5j satuan
c = 6i + 7j satuan
Tentukan besar resultan ketiga vektor, dan kemiringan sudut antara resultan dan sumbu X
Pembahasan!
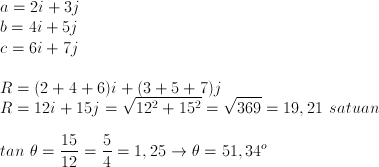
Untuk lebih jelas berikut ilustrasinya:

12 pada sumbu x
15 pada sumbu y
Arahnya adalah sudut θ yang bisa dicari dari sin θ, cos θ maupun tan θ. Jika dicari dari tan θ maka yang dibandingkan nilai pada sumbu y dengan nilai pada sumbu x. Jika dicari dari sin θ yang dibandingkan nilai pada sumbu y dengan nilai resultan R, jika digunakan cos θ bandingkan nilai pada sumbu x dengan nilai resultan R.
a) A⋅ B
b) A × BPembahasan!
a) A⋅ B adalah perkalian titik (dot) antara vektor A dan vektor B
Untuk perkalian titik berlaku
A⋅ B = A B cos θ
Sehingga
A⋅ B = A B cos 37° = (8)(10)(0,8) = 64 satuanb) A × B adalah perkalian silang (cross) vektor A dan vektor B
Untuk perkalian silang berlaku
A × B = A B sin θ
Sehingga
A × B = A B sin 37° = (8)(10)(0,6) = 48 satuan
B. 6
C. 7
D. 8
E. 12Pembahasan
Soal ini adalah soal penerapan perkalian titik (dot product ) antara vektor gaya F dan vektor perpindahan r dengan kedua vektor dalam bentuk i dan j atau vektor satuan. Besaran yang dihasilkan nantinya adalah skalar (usaha termasuk besaran skalar, hanya memiliki besar, tanpa arah). Usaha dilambangkan dengan W dari kata work.
W = F ⋅ r
26 = (2i + 3j)⋅ (4i + aj)Cara perkalian titik dua vektor dalam bentuk i,j adalah yang i kalikan i, yang j kalikan j, hingga seperti berikut
26 = 8 + 3a
3a = 26 − 8
a = 18/3 = 6
i dan j nya jadi hilang karena i kali i atau j kali j hasilnya adalah satu.
9.Diberikan dua buah vektor masing-masing:
A = 4i + 3j − 2k
B = 7i + 2j + 5k
Tentukan hasil dari A × B
Pembahasan
Perkalian silang, A × B
Misal :
A = (Ax i + Ay j + Az k) dan B = (Bx i + By j + Bz k)
maka :
| A × B = (Ay Bz − Az By) i + (Az Bx − Ax Bz) j + (Ax By − Ay Bx) k |
↑
Rumus Perkalian Silang Dua Vektor (cross product ) dalam i, j, k
Data :
A = 4i + 3j − 2k
B = 7i + 2j + 5k
| Ax = 4 Ay = 3 Az = − 2 |
Bx = 7 By = 2 Bz = 5 |
maka
A × B = (Ay Bz − Az By) i + (Az Bx − Ax Bz) j + (Ax By − Ay Bx) k
A × B = [(3)(5) − (−2)(2)] i + [(−2)(7) − (4)(5)]j + [(4)(2) − (3)(7)] k
A × B = (15 + 4)i + (−14 − 20)j + (8 − 21)k
A × B = 19 i −34 j − 13k
Lumayan repot kalau mau dihafal rumus perkalian di atas, alternatifnya dengan cara yang kedua,
10. Dua buah vektor kecepatan P dan Q masing-masing besarnya 40 m/s dan 20 m/s membentuk sudut 60°.

Tentukan selisih kedua vektor tersebut!
Pembahasan
Menentukan selisih dua buah vektor yang diketahui sudutnya:
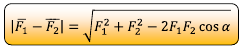
Sehingga